Not Wool Sequences

题面翻译

一个长度为 $n$ 的非负整数序列 $a_1,a_2,\ldots,a_n$ 称为 wool 序列，只要存在两个整数 $l$ 和 $r$（$1\leq l\leq r\leq n$）且 。换句话说，每个 wool 序列包含一个连续元素的子序列，其中异或值等于 $0$。

在这个问题中，我们要求您计算由 $0$ 到 $2^m - 1$ 的 $n$ 个整数组成的非 wool 序列的数目，并取模 $10^9+9$。

题目描述

A sequence of non-negative integers $ a_{1},a_{2},...,a_{n} $ of length $ n $ is called a wool sequence if and only if there exists two integers $ l $ and $ r $ $ (1<=l<=r<=n) $ such that . In other words each wool sequence contains a subsequence of consecutive elements with xor equal to 0.

The expression 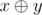means applying the operation of a bitwise xor to numbers $ x $ and $ y $ . The given operation exists in all modern programming languages, for example, in languages C++ and Java it is marked as "^", in Pascal — as "xor".

In this problem you are asked to compute the number of sequences made of $ n $ integers from 0 to $ 2^{m}-1 $ that are not a wool sequence. You should print this number modulo $ 1000000009 $ $ (10^{9}+9) $ .

输入格式

The only line of input contains two space-separated integers $ n $ and $ m $ $ (1<=n,m<=10^{5}) $ .

输出格式

Print the required number of sequences modulo $ 1000000009 $ $ (10^{9}+9) $ on the only line of output.

样例 #1

样例输入 #1

3 2

样例输出 #1

6

提示

Sequences of length $ 3 $ made of integers 0, 1, 2 and 3 that are not a wool sequence are (1, 3, 1), (1, 2, 1), (2, 1, 2), (2, 3, 2), (3, 1, 3) and (3, 2, 3).

题目分析

目的：求出非Wool序列的个数。

知识点：前缀和、异或

首先，考虑wool序列的特点，题面中解释的很清楚，为序列内存在连续元素的子序列，它们的异或值为 $0$。反过来说，非wool序列就是序列内不存在连续元素异或值为 $0$ 的子序列。

序列特征的关键在于连续区间的异或值，我们可以采用前缀和的思想进行快速求解。构造前缀异或的数组,即：

$$ s_i = \begin{cases} a_1 & i =1 \\ s_{i-1}\oplus a_i & 2\le i\le n \end{cases} $$

那么区间 $[L,R]$ 的异或值，可表达为 $s_R\oplus s_{L-1}$ 。结合异或的特性：两个数进行异或，当两者相同时，异或值为 $0$。也就是说当 $s_R$ 等于 $s_{L-1}$ 时，区间异或值为 $0$ 。序列中只要存在两个形同的前缀异或值，则为wool序列，反过来说，当序列中所有的前缀异或值都不相同时，就属于非wool序列了。

接下来考虑序列中所有的前缀异或值都不相同的序列数量。先去考虑前缀异或值的范围，题目告诉我们序列由 $0\sim 2^{m}-1$ 的整数构成，那么对应的前缀异或值的范围就是 $0\sim 2^m-1$。

来解释下前缀异或值的范围为什么是 $0\sim 2^m-1$。异或在计算时，二进制位相同为 $0$ 不同为 $1$，也被称作为不进位加法。所以两个非负整数 $a$ 和 $b$ 在异或计算时，结果的取值范围取决于两数中二进制的最高位的 $1$。若最高位 $1$ 的位置为 $k$ 则，最大的范围就是二进制中最低位到第 $k$ 位都是 $1$ 也就是 $2^{k+1}-1$。所以，当进行异或的元素值为 $0\sim 2^m-1$ 时，异或后的结果范围也是 $0\sim 2^m-1$。

由于我们现在找的序列要求是所有的前缀异或值都不相同，再结合子序列范围是 $1\le l\le r\le n$，包含了 $l=r$ 的情况，所以也要排除掉前缀异或值为 $0$ 的情况。那么问题就变成了从 $1\sim 2^m-1$ 中选择 $n$ 个数进行排列的方案数，即 $A_{2^m-1}^n$，也就是 $\prod\limits_{i=0}^{n-1}{2^m-1-i}$。

代码实现

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int M=1e9+9;
ll n,m,ans=1;
ll mypow(ll a,ll n){//快速幂
    ll ans=1;
    while(n){
        if(n&1){
            ans=ans*a;
            ans%=M;
        }
        a=a*a%M;
        n>>=1;
    }
    return ans;
}
int main()
{
    cin>>n>>m;
    ll tmp=mypow(2,m)-1;//先求出2^m - 1
    for(int i=0;i<n;i++){//求 A(2^m-1,n)
        ans=ans*(tmp-i)%M;
    }
    cout<<ans;
    return 0;
}